|
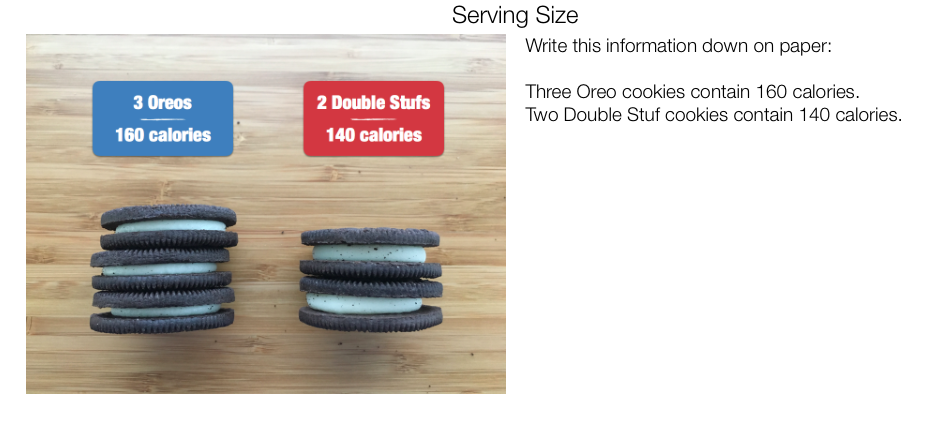
The typical response when I tell someone my major is usually along the lines of, oh my goodness, why would you ever want to do math for the rest of your life? I am currently working towards achieving a major in mathematics for secondary education but it's not because I am some math wiz. There was never a time that I just sat back in math class and aced my exams or quiz. I did well in math classes but it wasn't because I was super smart, it was because I worked hard to understand the concepts and studied a lot to do well in the classes. In my opinion, one of the biggest misconceptions in math classes is that you either you either have a math brain or you don't. That's the farthest from the truth, I wouldn't say I have math brain at all, I just know how to work hard to understand difficult topics; something anybody can learn. If you believe that you have the ability to understand a topic, you will understand it to a much further extent than someone who believes it's much too hard. In the book, Mathematic Mindsets, it talks about being gifted vs having a growth mindset. Everybody is born with the ability to learn math and the stereotype that only "gifted" people can learn math ruins the mindset for everyone else. On the flip side, people might grasp topics faster than others, but essentially we all have the ability to learn and understand math; no one is superior in learning. If people approached math with the right mindset, I think it would change people's experiences with it. Just believing that your brain has the ability to grow apposed to some people having gifts could be a big step in the right directions. I will play the devil's advocate because I know it's not all butterflies and rainbows if you work hard at something. There are a lot of people who just don't enjoy math and it's difficult to work hard at something you don't enjoy which essentially leads to people doing poorly in the class. In general, math can be very difficult and take a lot of practice which takes patience and hard work. I know that's not fun for everyone and especially when it takes longer amounts of time to grasp concepts; it's easy to get frustrated and give up. Here's the great thing about math, it can be applied to many real life situations, it's just not always portrayed that way. If math was taught in ways that were interesting to the class, it might be a little easier for them to work hard. Instead of just throwing numbers and practice problems on a white board, we could show the importance of what we're learning by applying it to the real world. Here's a quick video to give you an example of what I'm talking about... Instead of writing different equations on the board and showing different examples of parables you could show this video. This would be a perfect practice problem but gives students interest in what they're doing and keeps them focused on learning. Another really awesome resource is desmos. Desmos is a great tool that allows students to do hands on learning and gives application to what is being learned. Here's an example of a desmos activity with linear equations: This is the set up to the problem and get's the students interested in what problem they are going to try to figure out. I think it would be a good idea to bring the class in some Oreo's to snack on while they do this problem, it will allow math to become something real and tangible. You can flip through the slideshow below to see the rest of the problem. As they flip through the questions they can make predictions and it allows them to make and correct mistakes. At the end of the activity you can bring it together as a class to reflect on the things learned and discovered. This breaks up the amount of lecture time and keeps the class interested in what is being learned. It gives students the opportunity to learn on their own and then you can still bring it back and have a discussion. Just like the youtube video shown above, it gives students practice and they're not just listening to you talk about different types of graphs and functions.
To bring everything together, you see that with the right mindset and interest in what you're learning you can learn anything! As an educator, being creative in teaching as well as allowing students to have open minds can help set students up for success.
4 Comments
The beginning has begun; learning to teach future learners. In mathematics, when you learn something new it mostly like will be used to build of something else you're going to use in the future. Some of the first and most basic concepts you learn are used repeatedly throughout your career as student, such as fractions, addition, equations, linear functions and so on. As you use these things over the years, for some people, it starts to become second nature, something you don't really have to think about. When you're put in a situation where you have to think about your thinking, those second nature concepts become almost a challenge. You've been doing it for so long, it's not something you think about anymore. I am currently enrolled in Math 229, which is teaching middle grades math and I am also an SLA facilitator for Math 097, which is elementary algebra. I am also in three hundred level courses and yet I am being challenged equally by a 300 level course as a 097 and 229 course. How is that possible? Thinking about your thinking is difficult! Both 229 & 097 have forced me to think back to those surface level concepts and process how I solve those problems. Then on top of that, forcing myself to think about different ways to solve the problems and not just my "go to thinking." Why is that so important? Why do I need to know different ways to solve a problem and fully understand why I may solve a problem a certain way? I've already learned so much being an SLA facilitator and if one thing is true, it's that students need to be engaged for them to fully understand the concepts. The surface level concepts that are so crucial to the rest of the semester need to be taught and learned really well. This means that you can't move on to the bigger concepts until the class has mastered those first basic concepts. I've realized in Math 229 the importance of being able to explain things in many different ways. There are so many different kinds of learners and if you're teaching in one way, you might not reach half the class and therefore they may not be engaged in your teaching. For example, I could've sat through the same math classes for 6 years as Sue. Those concepts we learned became second nature to me because all our teachers gave lots of practice problems and that's how I learn best. Those same concepts are not second nature to Sally because she is a visual learner and needs thing to be applied to the real world in order for her to fully understand. Being engaged makes a difference in what you learn. As you can see, learning to teach to your audience is a big concept to grasp. In closing, how do you teach those crucial topics to students, keep them engaged in your instruction, and make sure your using many different methods in teaching it? A good question that I am still learning the answer too. I think it starts with establishing a teaching style, but being flexible enough to understand that it may change every year, or even every month. I have a youtube video below that discusses the importance of keeping students engaged and few ideas on how to do that. It's interesting to think that just changing a story problem to a topic that interests the class could change how much they're engaged in the concept your teaching. |
AuthorLauren C. Grimes Archives
November 2017
|