|
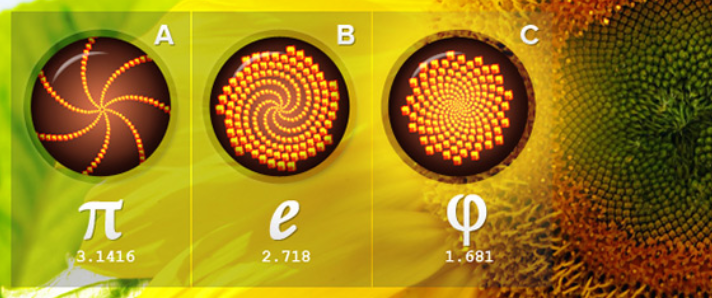
In an "ideal" math class (or any class for that matter) educators want students to be interested in the material and eager to learn the content. Am I right? That would be awesome if all students came to class each day excited about algebra and ready to learn! With that in mind, let's imagine you were required to attend a weekly work meeting on how to paint. There was no indication as to why you had to learn, but each week you were required to go to a class in order to learn how to paint. There will may individuals who like it and may do well with it, others who are neutral, and some that hate. But overall, the majority of those people will most likely be curious as to how it is relevant, why it's necessary, and how it will benefit it them. Don't you think your students are wondering the same thing? Stay with me here, consider about this example... You get hired into a company and they train you how to build a single part of an airplane. They give you all the details about that single part but nothing else. As you are making this part, some days you might get tired and not pay as much attention to detail or maybe you make the part and something looks a little off but you've had a rough day so you send it on anyway. In your head, you may be thinking it's just one part of the plane and it's not that big of a deal. BUT, what if your boss had given you a birds eye view of that part in relation to the plane as a whole. What if he explained that the part you are making is the most crucial part of the plane and told you all the reasons why it was important and how it effected other parts of the plane. Would you be motivated to try little harder? Would you pay more attention to detail? Would feel a stronger sense of responsibility to excel in your work? Let's dream for a second, will you dream with me?Kelsey York (a friend of mine) and myself are currently in the process of creating a curriculum that can be implemented into most math classes that allows students to widen their view of mathematics and develop accurate thoughts on mathematics as a whole (not just based on their 6th grade algebra class). Students are currently getting small snapshots of mathematics and basing their opinions of the subject strictly off of what they learn in class. I believe that if students developed opinions on mathematics that were based on the history of math, historical mathematicians, and topics that go beyond just math the would be more interested in what they were learning (sort of like the example above). So how does this work?We have created a 10 week curriculum that occurs once a week for anywhere from 30 to 45 minutes (depending on how much time you want to spend on it). The overall idea of the curriculum is for students to explore whether mathematics was invented or discovered. We laid out 8 exploratory lessons that allow students to learn about mathematicians, how their passions relate to math, how math applies to world around us, and other topics as well. At then end of each lesson students will journal and record their "take away from the lesson" which will include their current standing each week on whether math was invented or discovered. The first eight weeks students will being exploring different topics and trying to establish their own beliefs and views. On week nine, students will review their journals and notes to establish a more concrete idea of what they believe. Then on week ten, students will partake in a debate within the classroom on whether mathematics was invented or discovered. We chose to finish the curriculum with a debate because debates usually get people fired about a topic, whether they are truly invested in it or not. The hope is that this intrigues students and allows them to see the bigger picture of mathematics and how it applies to the personally. The general layout of the lessons is shown below and we've designed them in a way that allows you quickly alter and change how you present the information. We also created the eight lessons using two different structures for displaying the information so students wouldn't fall into a routine and miss important information. The outline allows for a small teaching, group or individual exploring while applying it to relevant aspects of student lives, and then a reflection. Welcome/Overview Introduction: 10-12 minutes Individual Activity: 2 minutes Partner/Group Activity: 3 minutes Application: 5 minutes Journal: 5 minutes So now that you've read the whole post, let's go back to the first two examples. Do they make more sense now? I want students to understand why math is important beyond the four walls of my classroom. I want them to see that math can be used to explain so many parts of our world and even the galaxies in the sky. It's so much bigger than just the small snapshots that they learn in class and I don't believe students know that, so can we teach them? Can we allow our students to discover that math is literally everywhere? Can we widen their perspectives and allow them to explore the world of math without any test, quizzes, or pressure? |
AuthorLauren C. Grimes Archives
November 2017
|